چگونه ریشه دوم عدد ۲ به یک عدد تبدیل شد؟!

یونانیان باستان می‌خواستند باور کنند که جهان را می‌توان به‌طور کامل با استفاده از اعداد صحیح و نسبت‌های بین آن‌ها – کسری که امروزه به آن اعداد گویا می‌گوییم – توصیف کرد. اما این آرزو زمانی که آن‌ها مربعی با اضلاع به طول ۱ در نظر گرفتند و متوجه شدند که طول قطر آن نمی‌تواند به‌صورت یک کسر نوشته شود، نقش بر آب شد.

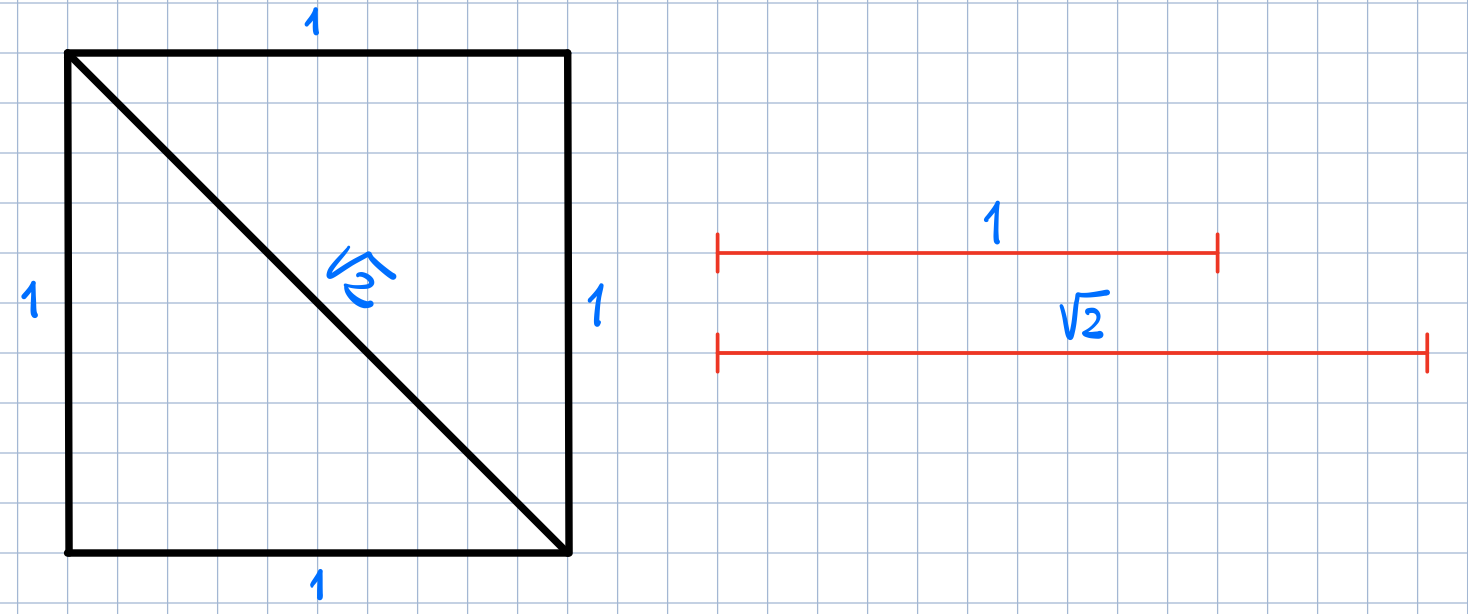
اولین اثبات این موضوع (که بعدها چندین اثبات دیگر نیز ارائه شد) معمولاً به فیثاغورس، فیلسوفی از قرن ششم قبل از میلاد، نسبت داده می‌شود، اگرچه هیچ‌یک از نوشته‌های او باقی نمانده و اطلاعات کمی درباره او در دست است. با این حال، «این اولین بحران در آنچه ما بنیان‌های ریاضیات می‌نامیم بود» به گفته جان بل (John Bell)، استاد بازنشسته در دانشگاه وسترن در لندن، انتاریو این بحران برای مدت زیادی حل نشد. اگرچه یونانیان باستان می‌توانستند مشخص کنند که \(\sqrt2\) چه چیزی نیست، اما متاسفانه زبانی برای توضیح دادن اینکه چه چیزی هست، نداشتند.

فیثاغورس فیلسوف قرن ششم قبل از میلاد- درحال فکر کردن

برای هزاران سال، همین وضعیت باقی ماند.  ریاضیدانان رنسانس با آنچه بعداً اعداد گنگ نامیدند، دست و پنجه نرم می‌کردند و در عین حال سعی در حل معادلات جبری داشتند. نمادهای امروزی برای ریشه‌های دوم در قرن‌های ۱۶ و ۱۷ به کار گرفته شد. اما همچنان چیزی مبهم درباره آن‌ها وجود داشت. آیا \(\sqrt2\) به همان شکلی که \(2\) وجود دارد، وجود داشت؟ مشخص نبود.

ریاضیدانان برای قرن ها با این ابهام کنار آمدند. سپس، در اواسط دهه 1800، ریاضیدانانی از جمله ریچارد ددکیند (Richard Dedekind) متوجه شدند که حسابان – که 200 سال قبل توسط اسحاق نیوتن (Isaac Newton) و گوتفرید لایب نیتس (Gottfried Leibniz) بنا شده بود – بر پایۀ استواری قرار ندارد. ددکیند، که ریاضیدان با استعداد اما محتاطی بود و به آرامی کار می کرد، یک روز در حال آماده سازی خود برای تدریس توابع پیوسته به دانشجویانش بود که فهمید نمی تواند توضیح رضایت بخشی در مورد مفهوم پیوستگی یک تابع ارائه دهد.

او حتی با تعریف درستی از توابع هم مواجه نشده بود. ددکیند بیان کرد که برای این کار ما باید ابتدا درک درستی از چگونگی کارکرد اعداد داشت باشیم. چیزی که به نظر می رسید ریاضیدانان آن را بدیهی فرض کرده اند. او پرسید که چطور می توان مطمئن شد که حاصلضرب \(\sqrt2\) در \(\sqrt3\) برابر با \(\sqrt6\) است؟ او می خواست پاسخ هایی برای این سوالات ارائه دهد.

بنابراین او روشی برای تعریف و ساختن اعداد گنگ با استفاده از تنها اعداد گویا معرفی کرد. روش او این‌گونه کار می‌کند: ابتدا تمام اعداد گویا را به دو مجموعه تقسیم کنید، به طوری که همه کسرهای یک مجموعه کوچکتر از مجموعه دیگر باشند. برای مثال، در یک مجموعه، تمام اعداد گویایی که وقتی به توان دو می‌رسند، کمتر از ۲ هستند را جمع‌آوری کنید؛ و در مجموعۀ دیگر، تمام اعداد گویایی که مربع آن‌ها بیشتر از ۲ است. دقیقاً یک عدد بین این دو مجموعه قرار می‌گیرد. ریاضی‌دانان به آن برچسب \(\sqrt2\) می‌دهند. بنابراین از نظر ددکیند، یک عدد گنگ با یک جفت مجموعه بی‌نهایت از اعداد گویا تعریف می‌شود. چیزی که او آن را “برش” می‌نامید. این یک ایده بسیار زیبا است. به گفته ایان استوارت (Ian Stewart) از دانشگاه وارویک. «شما می‌توانید اعداد گنگ مفقود را نه با توصیف آن‌ها، بلکه با توصیف شکاف‌هایی که باید در آن‌ها قرار بگیرند، مشخص کنید.»

ددکیند نشان داد که شما می‌توانید به این روش کل خط اعداد را پر کنید، و برای اولین بار به طور دقیق آنچه که اکنون اعداد حقیقی (ترکیبی از اعداد گویا و گنگ) می‌نامیم را تعریف کنید.

تقريبا همزمان با اينكه ددکيند روی روش برش های خودش کار می کرد، دوست و همکار او گئورگ كانتور (Georg Cantor) نيز شروع به فکر کردن در مورد اعداد گنگ کرد. این هم‌پوشانی رابطه آن‌ها را پیچیده کرد. لئو کوري، مورخ علم و رئيس دانشگاه، می گفت: «آنها دوستان خوبي بودند، اما از هم متنفر بودند. با هم همکاري مي کردند و از طرفی همديگر را ناديده مي گرفتند.»

کانتور تعریفی متفاوت از اعداد گنگ ارائه داد. او هر عدد گنگ را به صورت دنباله‌ای از اعداد گویا که به یک مقدار گنگ خاص نزدیک می‌شدند یا “همگرا می‌شدند” بیان کرد. اگرچه اعداد گنگ کانتور در ابتدا متفاوت از اعداد ددکیند به نظر می‌رسیدند، اما کارهای بعدی ثابت کردند که هر دو روش از نظر ریاضی معادل هستند.

کار کانتور او را به پرسیدن اینکه چند عدد وجود دارد هدایت کرد. این سؤال ممکن است در ابتدا عجیب به نظر برسد. اعداد صحیح بی‌نهایت بسیاری وجود دارند – شما همیشه می‌توانید یک عدد دیگر به آن اضافه کنید. احتمالاً، این بزرگ‌ترین مجموعه اعداد است که می‌تواند وجود داشته باشد. اما كانتور به طور متناقضی نشان داد که اگرچه تعداد کسرها با تعداد اعداد صحیح یکسان است، اما به طور قابل اثباتی تعداد اعداد گنگ بیشتری وجود دارد. او اولین کسی بود که متوجه شد بی نهایت در اندازه‌های مختلفی وجود دارد.

مسیر اعداد بیش از آنچه تصور می شد، شلوغ‌تر و عجیب‌تر بود. اما ریاضی‌دانان تنها پس از تغییر دیدگاه خود، قادر به دیدن این موضوع بودند.

برش‌های ددکیند را می‌توان به طور قطع سرآغاز ریاضیات مدرن دانست. استوارت می‌گوید: «این واقعاً اولین نقطه‌ای در تاریخ ریاضیات است که ریاضیدانان واقعاً می‌دانند درباره چه چیزی صحبت می‌کنند.» ددکیند و دیگران برای اولین بار از تعریف او برای اثبات قضایای اصلی در حساب استفاده کردند – که به آن‌ها اجازه می‌داد نه تنها بنای ریاضیدانی را که لایب‌نیتس و نیوتن ساخته بودند تقویت کنند، بلکه بر آن بیافزایند. کار ددکیند به ریاضیدانان کمک کرد تا توالی‌ها و توابع را بهتر درک کنند. تأثیر او در بسیاری از زمینه‌های ریاضی گسترده بود. گفته می‌شود امی نوتر، ریاضیدان پرکاری که به شکل‌گیری زمینه جبر مجرد در اوایل قرن بیستم کمک کرد، به دانش‌آموزانش گفته است که «همه چیز در حال حاضر در کار ددکیند وجود دارد.»

تعریف رسمی \(\sqrt2\) زمینه‌های جدیدی را برای کاوش فراتر از موضوعات حساب (calculus) که در ابتدا انگیزه دهنده ددکیند بود، باز کرد. همانطور که استوارت گفت، “بعد از ددکیند، ریاضیدانان شروع به درک این موضوع کردند که شما می توانید مفاهیم کاملاً جدیدی را اختراع کنید. … کل ایده ریاضیات بسیار گسترده تر و انعطاف پذیرتر می شود.”

منبع: www.quantamagazine.org